Students who have taken a course Calculus should recognize the Newton Raphson Method for finding zeros/roots of a differentiable function. In this page I show an expansion of this method that can be used to find the complex roots of a differentiable function. For example, the equation x^3=1 has 3 solutions, one of which is a real number. The Newton Raphson Method can also be used to find the complex roots of a function.

The Newton Raphson Method is an iterative method which takes a point, and then gives a new point which is hopefully closer to a zero of the function. The new point is then used to calculate the next iteration, and after applying the method a large number of times, we will most of the time converge upon a zero of the function.

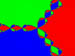
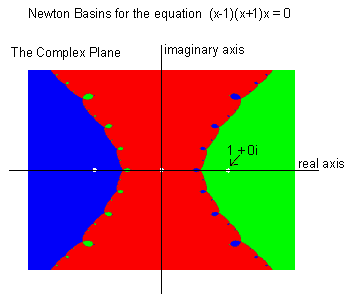
This page shows some images that graphically portray the regions of the complex plane which will converge to each of the roots of an equation. For example, if we start with any point in one of the blue regions in a picture below, we will converge to the root in a blue region. We call a Newton Attraction Basin the set of all points that converge to a specific root when used as initial points in the Newton Raphson method.

The following diagram shows the complex plane and three newton basins. If we pick any complex point in the green regions, when it is used as the initial point in the Newton Method, it will converge to the root 1+0i, which is labeled in the diagram.

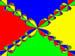
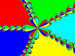
Next we have non-shaded versions of various basins. The roots are marked by small white spots. The equations that generate these simply are the product of (x-r1)(x-r2)...(x-rn)=0 where r1,r2,...,rn are the roots of this equation or the zeros of the left hand side of the equation. No complicated equations were used for any of these examples, but we interesting diagrams generated by simple equations.

3 roots: {-1,0,1}	5 roots: {0, 1, -1, i, -i}	5 roots: {0, 1, -1, i, -i} where 0 is a double root	5 roots: {1/2, 1, -1, i, -i}	6 roots: {1, -1, 1/2, -1/2, i, -i}	3rd roots of unity: {1, -1/2+sqrt(3)/2,-1/2-sqrt(3)/2}
4th roots of unity	5th roots of unity	6th roots of unity	7th roots of unity	8th roots of unity

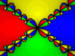
The following images are shaded representations of similar basins. Dark areas are areas where the given point doesn't converge quickly enough to a root. The darker areas converge more slowly the lighter areas do.

3 roots: {-1,0,1}	5 roots: {0, 1, -1, i, -i}	5 roots: {0, 1, -1, i, -i} where 0 is a double root	5 roots: {1/2, 1, -1, i, -i}	3 roots of unity: {1, -1/2+sqrt(3)/2,-1/2-sqrt(3)/2}	2 roots: {1/2+i/2, -1/2+i/2}
4th roots of unity	5th roots of unity	6th roots of unity	7th roots of unity	8th roots of unity