
Another Example
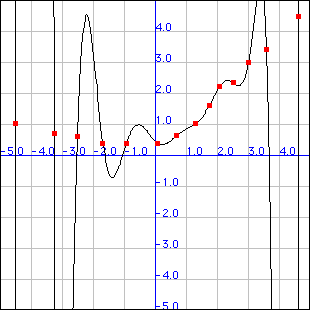
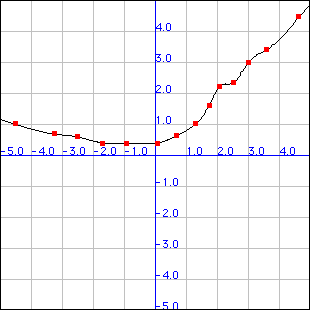
You can copy and paste these numbers directly into the applet. You might have to use control-c and control-v on your keyboard to copy and paste these numbers. The Lagrange Method for Polynomial Interpolation easily interpolates these points: It does show however the wide fluctuations on either end of the set of points. The wild behavior of the curves near the ends of the interval is inherent in the Lagrange Method. For situations with many points, where a "smoother" interpolation is needed, the natural cubic spline gives much nicer results:
We can use quite a few points with this applet. If you have a slow computer, this example might take a long time to process. Here is an example of 14 points forming a "smooth" curve:
-4.548387096774193,1.032258064516129
-3.290322580645161,0.7096774193548387
-0.9354838709677419,0.4193548387096774
-1.7096774193548387,0.4193548387096774
0.06451612903225806,0.4193548387096774
0.6774193548387096,0.6451612903225806
1.2903225806451613,1.032258064516129
1.7419354838709677,1.6129032258064515
2.064516129032258,2.225806451612903
2.5161290322580645,2.3548387096774195
3.0,3.0
3.5806451612903225,3.4193548387096775
4.64516129032258,4.483870967741935
-2.5161290322580645,0.6129032258064516
©2002-2003 Isaac Dooley